Regular Expression Matching Can Be Simple And Fast
(but is slow in Java, Perl, PHP, Python, Ruby, ...)
Introduction
This is a tale of two approaches to regular expression matching. One of them is in widespread use in the standard interpreters for many languages, including Perl. The other is used only in a few places, notably most implementations of awk and grep. The two approaches have wildly different performance characteristics:
 | |  |
|
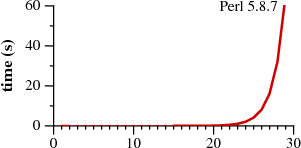
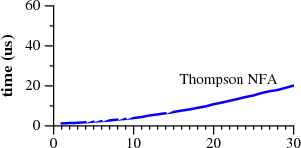
Time to match a?nan against an |
Let's use superscripts to denote string repetition, so that a?3a3 is shorthand for a?a?a?aaa. The two graphs plot the time required by each approach to match the regular expression a?nanagainst the string an.
Notice that Perl requires over sixty seconds to match a 29-character string. The other approach, labeled Thompson NFA for reasons that will be explained later, requires twentymicroseconds to match the string. That's not a typo. The Perl graph plots time in seconds, while the Thompson NFA graph plots time in microseconds: the Thompson NFA implementation is a million times faster than Perl when running on a miniscule 29-character string. The trends shown in the graph continue: the Thompson NFA handles a 100-character string in under 200 microseconds, while Perl would require over 1015 years. (Perl is only the most conspicuous example of a large number of popular programs that use the same algorithm; the above graph could have been Python, or PHP, or Ruby, or many other languages. A more detailed graph later in this article presents data for other implementations.)
It may be hard to believe the graphs: perhaps you've used Perl, and it never seemed like regular expression matching was particularly slow. Most of the time, in fact, regular expression matching in Perl is fast enough. As the graph shows, though, it is possible to write so-called "pathological" regular expressions that Perl matches very very slowly. In contrast, there are no regular expressions that are pathological for the Thompson NFA implementation. Seeing the two graphs side by side prompts the question, "why doesn't Perl use the Thompson NFA approach?" It can, it should, and that's what the rest of this article is about.
Historically, regular expressions are one of computer science's shining examples of how using good theory leads to good programs. They were originally developed by theorists as a simple computational model, but Ken Thompson introduced them to programmers in his implementation of the text editor QED for CTSS. Dennis Ritchie followed suit in his own implementation of QED, for GE-TSS. Thompson and Ritchie would go on to create Unix, and they brought regular expressions with them. By the late 1970s, regular expressions were a key feature of the Unix landscape, in tools such as ed, sed, grep, egrep, awk, and lex.
Today, regular expressions have also become a shining example of how ignoring good theory leads to bad programs. The regular expression implementations used by today's popular tools are significantly slower than the ones used in many of those thirty-year-old Unix tools.
This article reviews the good theory: regular expressions, finite automata, and a regular expression search algorithm invented by Ken Thompson in the mid-1960s. It also puts the theory into practice, describing a simple implementation of Thompson's algorithm. That implementation, less than 400 lines of C, is the one that went head to head with Perl above. It outperforms the more complex real-world implementations used by Perl, Python, PCRE, and others. The article concludes with a discussion of how theory might yet be converted into practice in the real-world implementations.
Regular Expressions
Regular expressions are a notation for describing sets of character strings. When a particular string is in the set described by a regular expression, we often say that the regular expressionmatches the string.
The simplest regular expression is a single literal character. Except for the special metacharacters *+?()|, characters match themselves. To match a metacharacter, escape it with a backslash: \+ matches a literal plus character.
Two regular expressions can be alternated or concatenated to form a new regular expression: if e1 matches s and e2 matches t, then e1|e2 matches s or t, and e1e2 matches st.
The metacharacters *, +, and ? are repetition operators: e1* matches a sequence of zero or more (possibly different) strings, each of which match e1; e1+ matches one or more; e1? matches zero or one.
The operator precedence, from weakest to strongest binding, is first alternation, then concatenation, and finally the repetition operators. Explicit parentheses can be used to force different meanings, just as in arithmetic expressions. Some examples: ab|cd is equivalent to (ab)|(cd); ab* is equivalent to a(b*).
The syntax described so far is a subset of the traditional Unix egrep regular expression syntax. This subset suffices to describe all regular languages: loosely speaking, a regular language is a set of strings that can be matched in a single pass through the text using only a fixed amount of memory. Newer regular expression facilities (notably Perl and those that have copied it) have addedmany new operators and escape sequences. These additions make the regular expressions more concise, and sometimes more cryptic, but usually not more powerful: these fancy new regular expressions almost always have longer equivalents using the traditional syntax.
One common regular expression extension that does provide additional power is called backreferences. A backreference like \1 or \2 matches the string matched by a previous parenthesized expression, and only that string: (cat|dog)\1 matches catcat and dogdog but not catdog nor dogcat. As far as the theoretical term is concerned, regular expressions with backreferences are not regular expressions. The power that backreferences add comes at great cost: in the worst case, the best known implementations require exponential search algorithms, like the one Perl uses. Perl (and the other languages) could not now remove backreference support, of course, but they could employ much faster algorithms when presented with regular expressions that don't have backreferences, like the ones considered above. This article is about those faster algorithms.
Finite Automata
Another way to describe sets of character strings is with finite automata. Finite automata are also known as state machines, and we will use "automaton" and "machine" interchangeably.
As a simple example, here is a machine recognizing the set of strings matched by the regular expression a(bb)+a:

A finite automaton is always in one of its states, represented in the diagram by circles. (The numbers inside the circles are labels to make this discussion easier; they are not part of the machine's operation.) As it reads the string, it switches from state to state. This machine has two special states: the start state s0 and the matching state s4. Start states are depicted with lone arrowheads pointing at them, and matching states are drawn as a double circle.
The machine reads an input string one character at a time, following arrows corresponding to the input to move from state to state. Suppose the input string is abbbba. When the machine reads the first letter of the string, the a, it is in the start state s0. It follows the a arrow to state s1. This process repeats as the machine reads the rest of the string: b to s2, b to s3, b to s2, b to s3, and finally a to s4.
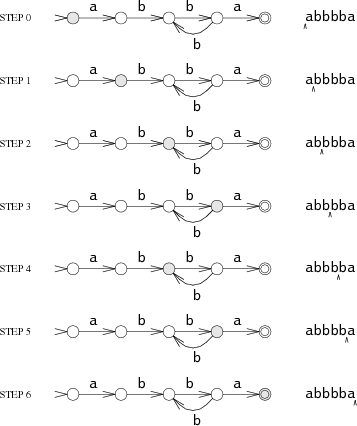
The machine ends in s4, a matching state, so it matches the string. If the machine ends in a non-matching state, it does not match the string. If, at any point during the machine's execution, there is no arrow for it to follow corresponding to the current input character, the machine stops executing early.
The machine we have been considering is called a deterministic finite automaton (DFA), because in any state, each possible input letter leads to at most one new state. We can also create machines that must choose between multiple possible next states. For example, this machine is equivalent to the previous one but is not deterministic:

The machine is not deterministic because if it reads a b in state s2, it has multiple choices for the next state: it can go back to s1 in hopes of seeing another bb, or it can go on to s3 in hopes of seeing the final a. Since the machine cannot peek ahead to see the rest of the string, it has no way to know which is the correct decision. In this situation, it turns out to be interesting to let the machine always guess correctly. Such machines are called non-deterministic finite automata (NFAs or NDFAs). An NFA matches an input string if there is some way it can read the string and follow arrows to a matching state.
Sometimes it is convenient to let NFAs have arrows with no corresponding input character. We will leave these arrows unlabeled. An NFA can, at any time, choose to follow an unlabeled arrow without reading any input. This NFA is equivalent to the previous two, but the unlabeled arrow makes the correspondence with a(bb)+a clearest:

Converting Regular Expressions to NFAs
Regular expressions and NFAs turn out to be exactly equivalent in power: every regular expression has an equivalent NFA (they match the same strings) and vice versa. (It turns out that DFAs are also equivalent in power to NFAs and regular expressions; we will see this later.) There are multiple ways to translate regular expressions into NFAs. The method described here was first described by Thompson in his 1968 CACM paper.
The NFA for a regular expression is built up from partial NFAs for each subexpression, with a different construction for each operator. The partial NFAs have no matching states: instead they have one or more dangling arrows, pointing to nothing. The construction process will finish by connecting these arrows to a matching state.
The NFAs for matching single characters look like:
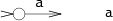
The NFA for the concatenation e1e2 connects the final arrow of the e1 machine to the start of the e2 machine:
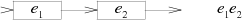
The NFA for the alternation e1|e2 adds a new start state with a choice of either the e1 machine or the e2 machine.
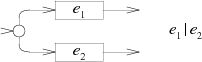
The NFA for e? alternates the e machine with an empty path:
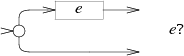
The NFA for e* uses the same alternation but loops a matching e machine back to the start:
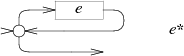
The NFA for e+ also creates a loop, but one that requires passing through e at least once:
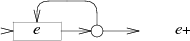
Counting the new states in the diagrams above, we can see that this technique creates exactly one state per character or metacharacter in the regular expression, excluding parentheses. Therefore the number of states in the final NFA is at most equal to the length of the original regular expression.
Just as with the example NFA discussed earlier, it is always possible to remove the unlabeled arrows, and it is also always possible to generate the NFA without the unlabeled arrows in the first place. Having the unlabeled arrows makes the NFA easier for us to read and understand, and they also make the C representation simpler, so we will keep them.
Regular Expression Search Algorithms
Now we have a way to test whether a regular expression matches a string: convert the regular expression to an NFA and then run the NFA using the string as input. Remember that NFAs are endowed with the ability to guess perfectly when faced with a choice of next state: to run the NFA using an ordinary computer, we must find a way to simulate this guessing.
One way to simulate perfect guessing is to guess one option, and if that doesn't work, try the other. For example, consider the NFA for abab|abbb run on the string abbb:
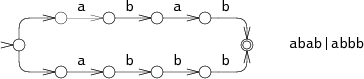
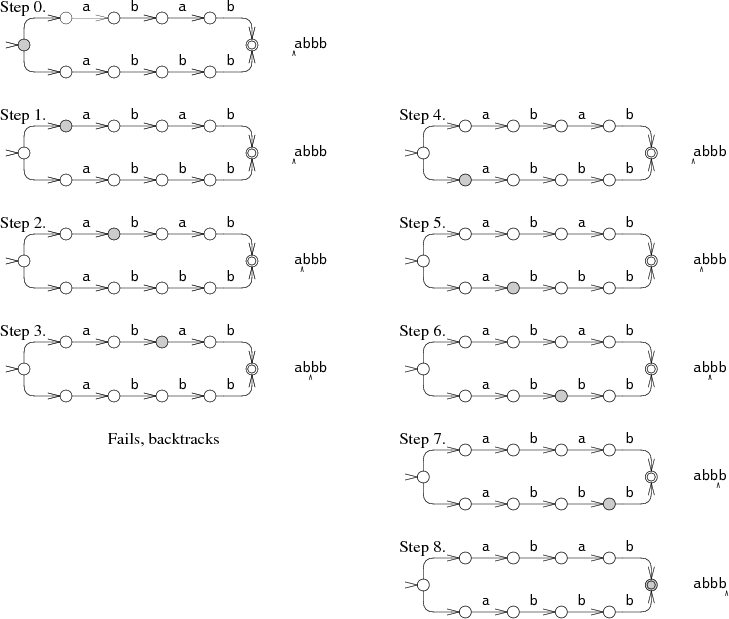
At step 0, the NFA must make a choice: try to match abab or try to match abbb? In the diagram, the NFA tries abab, but that fails after step 3. The NFA then tries the other choice, leading to step 4 and eventually a match. This backtracking approach has a simple recursive implementation but can read the input string many times before succeeding. If the string does not match, the machine must try all possible execution paths before giving up. The NFA tried only two different paths in the example, but in the worst case, there can be exponentially many possible execution paths, leading to very slow run times.
A more efficient but more complicated way to simulate perfect guessing is to guess both options simultaneously. In this approach, the simulation allows the machine to be in multiple states at once. To process each letter, it advances all the states along all the arrows that match the letter.
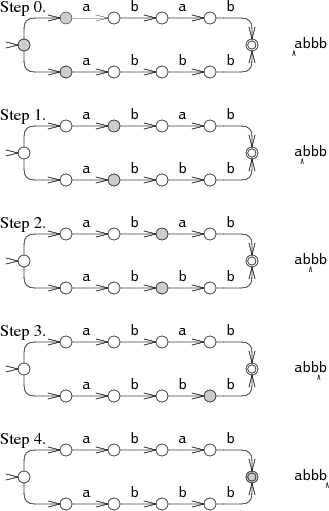
The machine starts in the start state and all the states reachable from the start state by unlabeled arrows. In steps 1 and 2, the NFA is in two states simultaneously. Only at step 3 does the state set narrow down to a single state. This multi-state approach tries both paths at the same time, reading the input only once. In the worst case, the NFA might be in every state at each step, but this results in at worst a constant amount of work independent of the length of the string, so arbitrarily large input strings can be processed in linear time. This is a dramatic improvement over the exponential time required by the backtracking approach. The efficiency comes from tracking the set of reachable states but not which paths were used to reach them. In an NFA with n nodes, there can only be n reachable states at any step, but there might be 2n paths through the NFA.
Implementation
Thompson introduced the multiple-state simulation approach in his 1968 paper. In his formulation, the states of the NFA were represented by small machine-code sequences, and the list of possible states was just a sequence of function call instructions. In essence, Thompson compiled the regular expression into clever machine code. Forty years later, computers are much faster and the machine code approach is not as necessary. The following sections present an implementation written in portable ANSI C. The full source code (under 400 lines) and the benchmarking scripts are available online. (Readers who are unfamiliar or uncomfortable with C or pointers should feel free to read the descriptions and skip over the actual code.)
Implementation: Compiling to NFA
The first step is to compile the regular expression into an equivalent NFA. In our C program, we will represent an NFA as a linked collection of State structures:
struct State { int c; State *out; State *out1; int lastlist; }; Each State represents one of the following three NFA fragments, depending on the value of c.
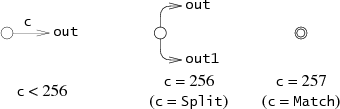
(Lastlist is used during execution and is explained in the next section.)
Following Thompson's paper, the compiler builds an NFA from a regular expression in postfix notation with dot (.) added as an explicit concatenation operator. A separate functionre2post rewrites infix regular expressions like "a(bb)+a" into equivalent postfix expressions like "abb.+.a.". (A "real" implementation would certainly need to use dot as the "any character" metacharacter rather than as a concatenation operator. A real implementation would also probably build the NFA during parsing rather than build an explicit postfix expression. However, the postfix version is convenient and follows Thompson's paper more closely.)
As the compiler scans the postfix expression, it maintains a stack of computed NFA fragments. Literals push new NFA fragments onto the stack, while operators pop fragments off the stack and then push a new fragment. For example, after compiling the abb in abb.+.a., the stack contains NFA fragments for a, b, and b. The compilation of the . that follows pops the two b NFA fragment from the stack and pushes an NFA fragment for the concatenation bb.. Each NFA fragment is defined by its start state and its outgoing arrows:
struct Frag { State *start; Ptrlist *out; }; Start points at the start state for the fragment, and out is a list of pointers to State* pointers that are not yet connected to anything. These are the dangling arrows in the NFA fragment.
Some helper functions manipulate pointer lists:
Ptrlist *list1(State **outp); Ptrlist *append(Ptrlist *l1, Ptrlist *l2); void patch(Ptrlist *l, State *s);
List1 creates a new pointer list containing the single pointer outp. Append concatenates two pointer lists, returning the result. Patch connects the dangling arrows in the pointer list l to the states: it sets *outp = s for each pointer outp in l.
Given these primitives and a fragment stack, the compiler is a simple loop over the postfix expression. At the end, there is a single fragment left: patching in a matching state completes the NFA.
State* post2nfa(char *postfix) { char *p; Frag stack[1000], *stackp, e1, e2, e; State *s; #define push(s) *stackp++ = s #define pop() *--stackp stackp = stack; for(p=postfix; *p; p++){ switch(*p){ /* compilation cases, described below */ } } e = pop(); patch(e.out, matchstate); return e.start; } The specific compilation cases mimic the translation steps described earlier.
Literal characters: default: s = state(*p, NULL, NULL); push(frag(s, list1(&s->out)); break; | 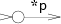 |
Catenation: case '.': e2 = pop(); e1 = pop(); patch(e1.out, e2.start); push(frag(e1.start, e2.out)); break; |  |
Alternation: case '|': e2 = pop(); e1 = pop(); s = state(Split, e1.start, e2.start); push(frag(s, append(e1.out, e2.out))); break; | 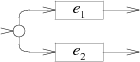 |
Zero or one: case '?': e = pop(); s = state(Split, e.start, NULL); push(frag(s, append(e.out, list1(&s->out1)))); break; | 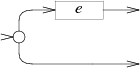 |
Zero or more: case '*': e = pop(); s = state(Split, e.start, NULL); patch(e.out, s); push(frag(s, list1(&s->out1))); break; | 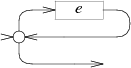 |
One or more: case '+': e = pop(); s = state(Split, e.start, NULL); patch(e.out, s); push(frag(e.start, list1(&s->out1))); break; | 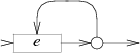 |
Implementation: Simulating the NFA
Now that the NFA has been built, we need to simulate it. The simulation requires tracking State sets, which are stored as a simple array list:
struct List { State **s; int n; }; The simulation uses two lists: clist is the current set of states that the NFA is in, and nlist is the next set of states that the NFA will be in, after processing the current character. The execution loop initializes clist to contain just the start state and then runs the machine one step at a time.
int match(State *start, char *s) { List *clist, *nlist, *t; /* l1 and l2 are preallocated globals */ clist = startlist(start, &l1); nlist = &l2; for(; *s; s++){ step(clist, *s, nlist); t = clist; clist = nlist; nlist = t; /* swap clist, nlist */ } return ismatch(clist); } To avoid allocating on every iteration of the loop, match uses two preallocated lists l1 and l2 as clist and nlist, swapping the two after each step.
If the final state list contains the matching state, then the string matches.
int ismatch(List *l) { int i; for(i=0; i<l->n; i++) if(l->s[i] == matchstate) return 1; return 0; } Addstate adds a state to the list, but not if it is already on the list. Scanning the entire list for each add would be inefficient; instead the variable listid acts as a list generation number. When addstate adds s to a list, it records lastid in s->lastlist. If the two are already equal, then s is already on the list being built. Addstate also follows unlabeled arrows: if s is aSplit state with two unlabeled arrows to new states, addstate adds those states to the list instead of s.
void addstate(List *l, State *s) { if(s == NULL || s->lastlist == listid) return; s->lastlist = listid; if(s->c == Split){ /* follow unlabeled arrows */ addstate(l, s->out); addstate(l, s->out1); return; } l->s[l->n++] = s; } Startlist creates an initial state list by adding just the start state:
List* startlist(State *s, List *l) { listid++; l->n = 0; addstate(l, s); return l; } Finally, step advances the NFA past a single character, using the current list clist to compute the next list nlist.
void step(List *clist, int c, List *nlist) { int i; State *s; listid++; nlist->n = 0; for(i=0; i<clist->n; i++){ s = clist->s[i]; if(s->c == c) addstate(nlist, s->out); } } Performance
The C implementation just described was not written with performance in mind. Even so, a slow implementation of a linear-time algorithm can easily outperform a fast implementation of an exponential-time algorithm once the exponent is large enough. Testing a variety of popular regular expression engines on a so-called pathological regular expression demonstrates this nicely.
Consider the regular expression a?nan. It matches the string an when the a? are chosen not to match any letters, leaving the entire string to be matched by the an. Backtracking regular expression implementations implement the zero-or-one ? by first trying one and then zero. There are n such choices to make, a total of 2n possibilities. Only the very last possibility—choosing zero for all the ?—will lead to a match. The backtracking approach thus requires O(2n) time, so it will not scale much beyond n=25.
In contrast, Thompson's algorithm maintains state lists of length approximately n and processes the string, also of length n, for a total of O(n2) time. (The run time is superlinear, because we are not keeping the regular expression constant as the input grows. For a regular expression of length m run on text of length n, the Thompson NFA requires O(mn) time.)
The following graph plots time required to check whether a?nan matches an:
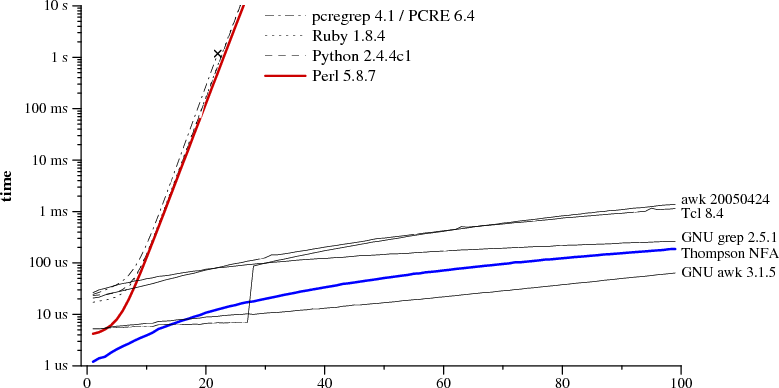
regular expression and text size n
a?nan matching an |
Notice that the graph's y-axis has a logarithmic scale, in order to be able to see a wide variety of times on a single graph.
From the graph it is clear that Perl, PCRE, Python, and Ruby are all using recursive backtracking. PCRE stops getting the right answer at n=23, because it aborts the recursive backtracking after a maximum number of steps. As of Perl 5.6, Perl's regular expression engine is said to memoize the recursive backtracking search, which should, at some memory cost, keep the search from taking exponential amounts of time unless backreferences are being used. As the performance graph shows, the memoization is not complete: Perl's run time grows exponentially even though there are no backreferences in the expression. Although not benchmarked here, Java uses a backtracking implementation too. In fact, the java.util.regex interface requires a backtracking implementation, because arbitrary Java code can be substituted into the matching path. PHP uses the PCRE library.
The thick blue line is the C implementation of Thompson's algorithm given above. Awk, Tcl, GNU grep, and GNU awk build DFAs, either precomputing them or using the on-the-fly construction described in the next section.
Some might argue that this test is unfair to the backtracking implementations, since it focuses on an uncommon corner case. This argument misses the point: given a choice between an implementation with a predictable, consistent, fast running time on all inputs or one that usually runs quickly but can take years of CPU time (or more) on some inputs, the decision should be easy. Also, while examples as dramatic as this one rarely occur in practice, less dramatic ones do occur. Examples include using (.*) (.*) (.*) (.*) (.*) to split five space-separated fields, or using alternations where the common cases are not listed first. As a result, programmers often learn which constructs are expensive and avoid them, or they turn to so-called optimizers. Using Thompson's NFA simulation does not require such adaptation: there are no expensive regular expressions.
Caching the NFA to build a DFA
Recall that DFAs are more efficient to execute than NFAs, because DFAs are only ever in one state at a time: they never have a choice of multiple next states. Any NFA can be converted into an equivalent DFA in which each DFA state corresponds to a list of NFA states.
For example, here is the NFA we used earlier for abab|abbb, with state numbers added:
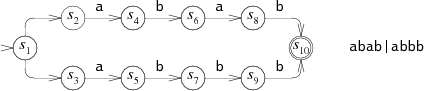
The equivalent DFA would be:
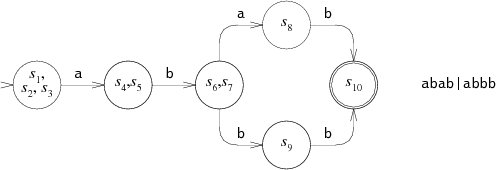
Each state in the DFA corresponds to a list of states from the NFA.
In a sense, Thompson's NFA simulation is executing the equivalent DFA: each List corresponds to some DFA state, and the step function is computing, given a list and a next character, the next DFA state to enter. Thompson's algorithm simulates the DFA by reconstructing each DFA state as it is needed. Rather than throw away this work after each step, we could cache theLists in spare memory, avoiding the cost of repeating the computation in the future and essentially computing the equivalent DFA as it is needed. This section presents the implementation of such an approach. Starting with the NFA implementation from the previous section, we need to add less than 100 lines to build a DFA implementation.
To implement the cache, we first introduce a new data type that represents a DFA state:
struct DState { List l; DState *next[256]; DState *left; DState *right; }; A DState is the cached copy of the list l. The array next contains pointers to the next state for each possible input character: if the current state is d and the next input character is c, then d->next[c] is the next state. If d->next[c] is null, then the next state has not been computed yet. Nextstate computes, records, and returns the next state for a given state and character.
The regular expression match follows d->next[c] repeatedly, calling nextstate to compute new states as needed.
int match(DState *start, char *s) { int c; DState *d, *next; d = start; for(; *s; s++){ c = *s & 0xFF; if((next = d->next[c]) == NULL) next = nextstate(d, c); d = next; } return ismatch(&d->l); } All the DStates that have been computed need to be saved in a structure that lets us look up a DState by its List. To do this, we arrange them in a binary tree using the sorted List as the key. The dstate function returns the DState for a given List, allocating one if necessary:
DState* dstate(List *l) { int i; DState **dp, *d; static DState *alldstates; qsort(l->s, l->n, sizeof l->s[0], ptrcmp); /* look in tree for existing DState */ dp = &alldstates; while((d = *dp) != NULL){ i = listcmp(l, &d->l); if(i < 0) dp = &d->left; else if(i > 0) dp = &d->right; else return d; } /* allocate, initialize new DState */ d = malloc(sizeof *d + l->n*sizeof l->s[0]); memset(d, 0, sizeof *d); d->l.s = (State**)(d+1); memmove(d->l.s, l->s, l->n*sizeof l->s[0]); d->l.n = l->n; /* insert in tree */ *dp = d; return d; } Nextstate runs the NFA step and returns the corresponding DState:
DState* nextstate(DState *d, int c) { step(&d->l, c, &l1); return d->next[c] = dstate(&l1); } Finally, the DFA's start state is the DState corresponding to the NFA's start list:
DState* startdstate(State *start) { return dstate(startlist(start, &l1)); } (As in the NFA simulation, l1 is a preallocated List.)
The DStates correspond to DFA states, but the DFA is only built as needed: if a DFA state has not been encountered during the search, it does not yet exist in the cache. An alternative would be to compute the entire DFA at once. Doing so would make match a little faster by removing the conditional branch, but at the cost of increased startup time and memory use.
One might also worry about bounding the amount of memory used by the on-the-fly DFA construction. Since the DStates are only a cache of the step function, the implementation ofdstate could choose to throw away the entire DFA so far if the cache grew too large. This cache replacement policy only requires a few extra lines of code in dstate and in nextstate, plus around 50 lines of code for memory management. An implementation is available online. (Awk uses a similar limited-size cache strategy, with a fixed limit of 32 cached states; this explains the discontinuity in its performance at n=28 in the graph above.)
NFAs derived from regular expressions tend to exhibit good locality: they visit the same states and follow the same transition arrows over and over when run on most texts. This makes the caching worthwhile: the first time an arrow is followed, the next state must be computed as in the NFA simulation, but future traversals of the arrow are just a single memory access. Real DFA-based implementations can make use of additional optimizations to run even faster. A companion article (not yet written) will explore DFA-based regular expression implementations in more detail.
Real world regular expressions
Regular expression usage in real programs is somewhat more complicated than what the regular expression implementations described above can handle. This section briefly describes the common complications; full treatment of any of these is beyond the scope of this introductory article.
Character classes. A character class, whether [0-9] or \w or . (dot), is just a concise representation of an alternation. Character classes can be expanded into alternations during compilation, though it is more efficient to add a new kind of NFA node to represent them explicitly. POSIX defines special character classes like [[:upper:]] that change meaning depending on the current locale, but the hard part of accommodating these is determining their meaning, not encoding that meaning into an NFA.
Escape sequences. Real regular expression syntaxes need to handle escape sequences, both as a way to match metacharacters (\(, \), \\, etc.) and to specify otherwise difficult-to-type characters such as \n.
Counted repetition. Many regular expression implementations provide a counted repetition operator {n} to match exactly n strings matching a pattern; {n,m} to match at least n but no more than m; and {n,} to match n or more. A recursive backtracking implementation can implement counted repetition using a loop; an NFA or DFA-based implementation must expand the repetition: e{3} expands to eee; e{3,5} expands to eeee?e?, and e{3,} expands to eee+.
Submatch extraction. When regular expressions are used for splitting or parsing strings, it is useful to be able to find out which sections of the input string were matched by each subexpression. After a regular expression like ([0-9]+-[0-9]+-[0-9]+) ([0-9]+:[0-9]+) matches a string (say a date and time), many regular expression engines make the text matched by each parenthesized expression available. For example, one might write in Perl:
if(/([0-9]+-[0-9]+-[0-9]+) ([0-9]+:[0-9]+)/){ print "date: $1, time: $2\n"; } The extraction of submatch boundaries has been mostly ignored by computer science theorists, and it is perhaps the most compelling argument for using recursive backtracking. However, Thompson-style algorithms can be adapted to track submatch boundaries without giving up efficient performance. The Eighth Edition Unix regexp(3) library implemented such an algorithm as early as 1985, though as explained below, it was not very widely used or even noticed.
Unanchored matches. This article has assumed that regular expressions are matched against an entire input string. In practice, one often wishes to find a substring of the input that matches the regular expression. Unix tools traditionally return the longest matching substring that starts at the leftmost possible point in the input. An unanchored search for e is a special case of submatch extraction: it is like searching for .*(e).* where the first .* is constrained to match as short a string as possible.
Non-greedy operators. In traditional Unix regular expressions, the repetition operators ?, *, and + are defined to match as much of the string as possible while still allowing the entire regular expression to match: when matching (.+)(.+) against abcd, the first (.+) will match abc, and the second will match d. These operators are now called greedy. Perl introduced ??, *?, and +?as non-greedy versions, which match as little of the string as possible while preserving the overall match: when matching (.+?)(.+?) against abcd, the first (.+?) will match only a, and the second will match bcd. By definition, whether an operator is greedy cannot affect whether a regular expression matches a particular string as a whole; it only affects the choice of submatch boundaries. The backtracking algorithm admits a simple implementation of non-greedy operators: try the shorter match before the longer one. For example, in a standard backtracking implementation, e? first tries using e and then tries not using it; e?? uses the other order. The submatch-tracking variants of Thompson's algorithm can be adapted to accommodate non-greedy operators.
Assertions. The traditional regular expression metacharacters ^ and $ can be viewed as assertions about the text around them: ^ asserts that the previous character is a newline (or the beginning of the string), while $ asserts that the next character is a newline (or the end of the string). Perl added more assertions, like the word boundary \b, which asserts that the previous character is alphanumeric but the next is not, or vice versa. Perl also generalized the idea to arbitrary conditions called lookahead assertions: (?=re) asserts that the text after the current input position matches re, but does not actually advance the input position; (?!re) is similar but asserts that the text does not match re. The lookbehind assertions (?<=re) and (?<!re) are similar but make assertions about the text before the current input position. Simple assertions like ^, $, and \b are easy to accommodate in an NFA, delaying the match one byte for forward assertions. The generalized assertions are harder to accommodate but in principle could be encoded in the NFA.
Backreferences. As mentioned earlier, no one knows how to implement regular expressions with backreferences efficiently, though no one can prove that it's impossible either. (Specifically, the problem is NP-complete, meaning that if someone did find an efficient implementation, that would be major news to computer scientists and would win a million dollar prize.) The simplest, most effective strategy for backreferences, taken by the original awk and egrep, is not to implement them. This strategy is no longer practical: users have come to rely on backreferences for at least occasional use, and backreferences are part of the POSIX standard for regular expressions. Even so, it would be reasonable to use Thompson's NFA simulation for most regular expressions, and only bring out backtracking when it is needed. A particularly clever implementation could combine the two, resorting to backtracking only to accommodate the backreferences.
Backtracking with memoization. Perl's approach of using memoization to avoid exponential blowup during backtracking when possible is a good one. At least in theory, it should make Perl's regular expressions behave more like an NFA and less like backtracking. Memoization does not completely solve the problem, though: the memoization itself requires a memory footprint roughly equal to the size of the text times the size of the regular expression. Memoization also does not address the issue of the stack space used by backtracking, which is linear in the size of the text: matching long strings typically causes a backtracking implementation to run out of stack space:
$ perl -e '("a" x 100000) =~ /^(ab?)*$/;' Segmentation fault (core dumped) $ Character sets. Modern regular expression implementations must deal with large non-ASCII character sets such as Unicode. The Plan 9 regular expression library incorporates Unicode by running an NFA with a single Unicode character as the input character for each step. That library separates the running of the NFA from decoding the input, so that the same regular expression matching code is used for both UTF-8 and wide-character inputs.
History and References
Michael Rabin and Dana Scott introduced non-deterministic finite automata and the concept of non-determinism in 1959 [7], showing that NFAs can be simulated by (potentially much larger) DFAs in which each DFA state corresponds to a set of NFA states. (They won the Turing Award in 1976 for the introduction of the concept of non-determinism in that paper.)
R. McNaughton and H. Yamada [4] and Ken Thompson [9] are commonly credited with giving the first constructions to convert regular expressions into NFAs, even though neither paper mentions the then-nascent concept of an NFA. McNaughton and Yamada's construction creates a DFA, and Thompson's construction creates IBM 7094 machine code, but reading between the lines one can see latent NFA constructions underlying both. Regular expression to NFA constructions differ only in how they encode the choices that the NFA must make. The approach used above, mimicking Thompson, encodes the choices with explicit choice nodes (the Split nodes above) and unlabeled arrows. An alternative approach, the one most commonly credited to McNaughton and Yamada, is to avoid unlabeled arrows, instead allowing NFA states to have multiple outgoing arrows with the same label. McIlroy [3] gives a particularly elegant implementation of this approach in Haskell.
Thompson's regular expression implementation was for his QED editor running on the CTSS [10] operating system on the IBM 7094. A copy of the editor can be found in archived CTSS sources [5]. L. Peter Deutsch and Butler Lampson [1] developed the first QED, but Thompson's reimplementation was the first to use regular expressions. Dennis Ritchie, author of yet another QED implementation, has documented the early history of the QED editor [8] (Thompson, Ritchie, and Lampson later won Turing awards for work unrelated to QED or finite automata.)
Thompson's paper marked the beginning of a long line of regular expression implementations. Thompson chose not to use his algorithm when implementing the text editor ed, which appeared in First Edition Unix (1971), or in its descendant grep, which first appeared in the Fourth Edition (1973). Instead, these venerable Unix tools used recursive backtracking! Backtracking was justifiable because the regular expression syntax was quite limited: it omitted grouping parentheses and the |, ?, and + operators. Al Aho's egrep, which first appeared in the Seventh Edition (1979), was the first Unix tool to provide the full regular expression syntax, using a precomputed DFA. By the Eighth Edition (1985), egrep computed the DFA on the fly, like the implementation given above.
While writing the text editor sam [6] in the early 1980s, Rob Pike wrote a new regular expression implementation, which Dave Presotto extracted into a library that appeared in the Eighth Edition. Pike's implementation incorporated submatch tracking into an efficient NFA simulation but, like the rest of the Eighth Edition source, was not widely distributed. Pike himself did not realize that his technique was anything new. Henry Spencer reimplemented the Eighth Edition library interface from scratch, but using backtracking, and released his implementation into the public domain. It became very widely used, eventually serving as the basis for the slow regular expression implementations mentioned earlier: Perl, PCRE, Python, and so on. (In his defense, Spencer knew the routines could be slow, and he didn't know that a more efficient algorithm existed. He even warned in the documentation, "Many users have found the speed perfectly adequate, although replacing the insides of egrep with this code would be a mistake.") Pike's regular expression implementation, extended to support Unicode, was made freely available with sam in late 1992, but the particularly efficient regular expression search algorithm went unnoticed. The code is now available in many forms: as part of sam, as Plan 9's regular expression library, or packaged separately for Unix. Ville Laurikari independently discovered Pike's algorithm in 1999, developing a theoretical foundation as well [2].
Finally, any discussion of regular expressions would be incomplete without mentioning Jeffrey Friedl's book Mastering Regular Expressions, perhaps the most popular reference among today's programmers. Friedl's book teaches programmers how best to use today's regular expression implementations, but not how best to implement them. What little text it devotes to implementation issues perpetuates the widespread belief that recursive backtracking is the only way to simulate an NFA. Friedl makes it clear that he neither understands nor respects the underlying theory.
Summary
Regular expression matching can be simple and fast, using finite automata-based techniques that have been known for decades. In contrast, Perl, PCRE, Python, Ruby, Java, and many other languages have regular expression implementations based on recursive backtracking that are simple but can be excruciatingly slow. With the exception of backreferences, the features provided by the slow backtracking implementations can be provided by the automata-based implementations at dramatically faster, more consistent speeds.
The next article in this series, "Regular Expression Matching: the Virtual Machine Approach," discusses NFA-based submatch extraction. The final article, "Regular Expression Matching in the Wild," examines a production implementation.
Acknowledgements
Lee Feigenbaum, James Grimmelmann, Alex Healy, William Josephson, and Arnold Robbins read drafts of this article and made many helpful suggestions. Rob Pike clarified some of the history surrounding his regular expression implementation. Thanks to all.
References
[1] L. Peter Deutsch and Butler Lampson, "An online editor," Communications of the ACM 10(12) (December 1967), pp. 793–799. http://doi.acm.org/10.1145/363848.363863
[2] Ville Laurikari, "NFAs with Tagged Transitions, their Conversion to Deterministic Automata and Application to Regular Expressions," in Proceedings of the Symposium on String Processing and Information Retrieval, September 2000. http://laurikari.net/ville/spire2000-tnfa.ps
[3] M. Douglas McIlroy, "Enumerating the strings of regular languages," Journal of Functional Programming 14 (2004), pp. 503–518. http://www.cs.dartmouth.edu/~doug/nfa.ps.gz (preprint)
[4] R. McNaughton and H. Yamada, "Regular expressions and state graphs for automata," IRE Transactions on Electronic Computers EC-9(1) (March 1960), pp. 39–47.
[5] Paul Pierce, "CTSS source listings." http://www.piercefuller.com/library/ctss.html (Thompson's QED is in the file com5 in the source listings archive and is marked as 0QED)
[6] Rob Pike, "The text editor sam," Software—Practice & Experience 17(11) (November 1987), pp. 813–845. http://plan9.bell-labs.com/sys/doc/sam/sam.html
[7] Michael Rabin and Dana Scott, "Finite automata and their decision problems," IBM Journal of Research and Development 3 (1959), pp. 114–125.http://www.research.ibm.com/journal/rd/032/ibmrd0302C.pdf
[8] Dennis Ritchie, "An incomplete history of the QED text editor." http://plan9.bell-labs.com/~dmr/qed.html
[9] Ken Thompson, "Regular expression search algorithm," Communications of the ACM 11(6) (June 1968), pp. 419–422. http://doi.acm.org/10.1145/363347.363387 (PDF)
[10] Tom Van Vleck, "The IBM 7094 and CTSS." http://www.multicians.org/thvv/7094.html
Discussion on reddit and perlmonks and LtU
Copyright © 2007 Russ Cox. All Rights Reserved.
http://swtch.com/~rsc/regexp/
 此主题相关图片如下:瓶子.jpg (45KB)
此主题相关图片如下:瓶子.jpg (45KB)



















